Example 8.6.1. Solving an Exponential Equation.
Consider the exponential equation
\begin{equation*}
5^x = 10\text{.}
\end{equation*}
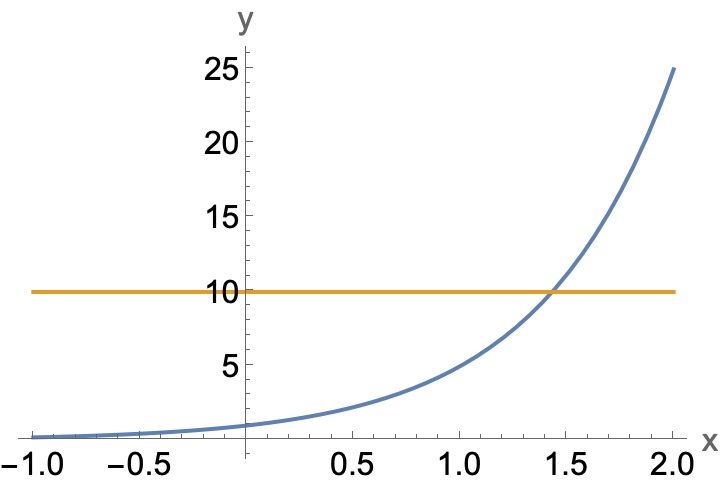
First observe that this equation must have a unique solution. This is because the exponential function \(f(x)=5^x\) is one-to-one. In the figure below it appears that the graph of \(y =10\) crosses \(y=5^x\) exactly once somewhere near \(x\approx 1.5\text{.}\)
On the one hand, we can rewrite the equation in logarithmic form to obtain
\begin{equation*}
5^{\boxed{x}} = 10 \quad \Rightarrow \quad \boxed{x} = \log_5(10)\text{.}
\end{equation*}
So that the solution is a logarithm. Unfortunately, your calculator is unlikely to have the ability to estimate base 5 logarithms.
Alternatively, we can express the solution in terms of the natural logarithm. Apply the natural logarithm to both sides to obtain an equivalent equation:
\begin{gather*}
5^x = 10\\
\ln(5^x) = \ln(10)
\end{gather*}
Use the power property of logarithms and solve for \(x\)
\begin{gather*}
x \cdot \ln(5) = \ln(10)\\
x = \frac{\ln(10)}{\ln(5)}
\end{gather*}
Thus, it must be that our base 5 answer is equal to this ratio of natural logarithms:
\begin{equation*}
x = \log_5(10) = \frac{\ln(10)}{\ln(5)}
\end{equation*}
We can now estimate with a calculator by diving the two logs.
\begin{equation*}
x = \log_5(10) \approx 1.431.
\end{equation*}
In exponential form,
\begin{equation*}
5^{1.431} \approx 10.
\end{equation*}

