Exercises

Exercises 9.7 Exercises

Exercises: Trig Functions.

These exercises address the six trigonometric functions of an angle $\theta$ in standard position as determined by the coordinates of a point on its terminal ray.
\begin{equation*} \sin(\theta) = \frac{y}{r}, \quad \cos(\theta) = \frac{x}{r}, \quad \tan(\theta) = \frac{y}{x} \end{equation*}
and their reciprocals
\begin{equation*} \csc(\theta) = \frac{r}{y} = \frac{1}{\sin(\theta)}, \quad \sec(\theta) = \frac{r}{x} = \frac{1}{\cos(\theta)}, \quad \cot(\theta) = \frac{x}{y} = \frac{1}{\tan(\theta)}. \end{equation*}

1.

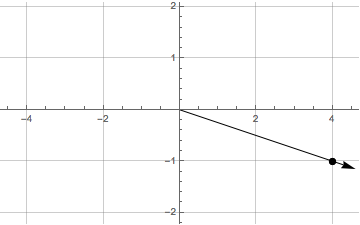
Find all six trigonometric function values of the angle $\theta$ in standard position whose terminal ray passes through the point $(x,y) = (4,-1)\text{.}$ See figure below.

Answer.

Table 9.33.

$\sin \theta = \frac{-1}{\sqrt{17}}= -\frac{\sqrt{17}}{17}$	$\csc \theta = \frac{\sqrt{17}}{-1} = - \sqrt{17}$
$\cos \theta = \frac{4}{\sqrt{17}}=\frac{4\sqrt{17}}{17}$	$\sec \theta = \frac{\sqrt{17}}{4}$
$\tan \theta = -\frac{1}{4}$	$\cot \theta = \frac{4}{-1}=-4$

Solution.

We need the radial distance $r$ from the origin to the point:

\begin{equation*} r^2 = 4^2 + (-1)^2 = 16 + 1 = 17 \Rightarrow r = \sqrt{17}. \end{equation*}

We can now form all the ratios we want with $x=4\text{,}$ $y = -1\text{,}$ and $r = \sqrt{17}$

Table 9.34.

$\sin \theta = \frac{-1}{\sqrt{17}}= -\frac{\sqrt{17}}{17}$	$\csc \theta = \frac{\sqrt{17}}{-1} = - \sqrt{17}$
$\cos \theta = \frac{4}{\sqrt{17}}=\frac{4\sqrt{17}}{17}$	$\sec \theta = \frac{\sqrt{17}}{4}$
$\tan \theta = -\frac{1}{4}$	$\cot \theta = \frac{4}{-1}=-4$

2.

Using a calculator, approximate the coordinates $(x,y)$ of the point on the circle indicated in the figure below.

Hint.

The radius of the circle appears to be $r = 4$

Answer.

$x \approx -2.06015$ and $y \approx 3.42867$

Solution.

The radius of the circle appears to be $r = 4\text{.}$ Using a calculator, $x = 4\times\cos (121^\circ) \approx -2.06015$ and $y = 4\times\sin (121^\circ) \approx 3.42867\text{.}$ Observe the signs of each are consistent with an angle in Quadrant II.

3.

Suppose $\theta$ is an angle in standard position whose terminal ray is in Quadrant III satisfying $\tan (\theta) = 3\text{.}$ Find the sine and cosine of $\theta\text{.}$

Answer.

$\sin \theta = -\frac{3\sqrt{10}}{10}$ and $\cos \theta = -\frac{\sqrt{10}}{10}.$

Solution.

Suppose $(x,y)$ is a point in the terminal ray of $\theta\text{.}$ Here’s what we know:

$x \lt 0$ is negative;
$y \lt 0$ is negative;
$\displaystyle \tan \theta = \frac{y}{x} = 3.$

So if $x = -1$ (negative), then $y = 3 x = -3\text{.}$ The point $(x,y) = (-1,-3)$ will do. (There are many other options!) The radial distance is

\begin{equation*} r^2 = (-1)^2 + (-3)^2 = 1 + 9 = 10 \Rightarrow r = \sqrt{10}. \end{equation*}

So,

\begin{equation*} \sin \theta = y/r = -3/\sqrt{10} = -\frac{3\sqrt{10}}{10} \end{equation*}

and

\begin{equation*} \cos \theta = x/r = -1/\sqrt{10} = -\frac{\sqrt{10}}{10}. \end{equation*}

4.

Suppose $\theta$ is an angle in standard position whose terminal ray is in Quadrant III satisfying $\sin (\theta) = -1/3\text{.}$ Find the cosine and tangent of $\theta\text{.}$

Answer.

$\cos \theta = -\sqrt{8}/3$ and $\tan \theta = \frac{\sqrt{8}}{8}$

Solution.

Suppose $(x,y)$ is a point in the terminal ray of $\theta\text{.}$ Here’s what we know:

$x \lt 0$ is negative;
$y \lt 0$ is negative;
$\displaystyle \sin \theta = \frac{y}{r} = -1/3.$

So if $y = -1$ (negative), then $r = 3\text{.}$ The $x$-coordinate must satisfy

\begin{equation*} r^2 = x^2 + y^2 \Rightarrow x^2 = 3^2 - (-1)^2 = 8 \Rightarrow x = \pm \sqrt{8} \end{equation*}

and since $x$ must be negative, we choose $x=-\sqrt{8}\text{.}$ The point $(-\sqrt{8},-1)$ is on the terminal ray of our angle. (There are many other options!) So,

\begin{equation*} \cos \theta = x/r = -\sqrt{8}/3 \end{equation*}

and

\begin{equation*} \tan \theta = y/x = \frac{-1}{-\sqrt{8}} = \frac{1}{\sqrt{8}} = \frac{\sqrt{8}}{8} \end{equation*}

5.

Suppose the terminal ray of an angle $\theta$ in standard position is in Quadrant IV. Which of the six trigonometric function values of $\theta$ are positive?

Solution.

In Quadrant IV, $x \gt 0$ is positive and $y \lt 0$ is negative. Thus,

Sine is negative; and so is its reciprocal cosecant.
Cosine is positive; and so is its reciprocal secant.
Tangent is negative; and so is its reciprocal cotangent.

Exercises: Unit Circle Trig.

These exercises address the connection between sine, cosine, and tangent and the geometry of the unit circle. We can use the reference angle and symmetry to find trigonometric functions of an angle.

\begin{equation*} \boxed{\sin(\theta) = \text{($y$-coordinate)}, \quad \cos(\theta) = \text{($x$-coordinate)}, \quad \tan(\theta) = \text{(slope of terminal ray)}} \end{equation*}

6.

Suppose $\theta$ is an angle in standard position. Explain what $\cos (\theta)\text{,}$ $\sin(\theta)\text{,}$ and $\tan(\theta)$ represent geometrically in relation to the unit circle $x^2+ y^2 = 1\text{.}$

Solution.

$\cos\theta$ is the $x$-coordinate of the point on the unit circle;
$\sin\theta$ is the $y$-coordinate of the point on the unit circle;
$\tan\theta$ is the slope of the line parallel to the terminal ray of $\theta\text{.}$

7.

Find the sine, cosine, and tangent of $\theta = -90^\circ\text{,}$ $\theta = 3\pi/2\text{,}$ and $\theta = 5\pi$ by considering the corresponding the geometry of the unit circle.

Solution.

The terminal ray of $\theta = -90^\circ$ intersects the unit circle at $(x,y) = (0,-1)\text{.}$ So
\begin{equation*} \sin(-90^\circ) = -1, \quad \cos(-90^\circ) = 0, \quad \tan(-90^\circ) \, \rm undefined \end{equation*}
Observe that the terminal ray is vertical so that it has no defined slope.
The terminal ray of $\theta = 3\pi/2$ is the same as $-90^\circ\text{.}$ Therefore,
\begin{equation*} \sin(3\pi/2) = -1, \quad \cos(3\pi/2) = 0, \quad \tan(3\pi/2) \, \rm undefined \end{equation*}
The terminal ray of $\theta = 5\pi$ intersects the unit circle at $(x,y) = (-1,0)\text{.}$ So
\begin{equation*} \sin(5\pi) = 0, \quad \cos(5\pi) = -1, \quad \tan(5\pi) = 0. \end{equation*}
Observe that the terminal ray is horizontal so that it has slope zero.

8.

Use the reference angle approach to find the six trigonometric function values of $\theta = 150^\circ\text{,}$ $\theta = -2\pi/3\text{,}$ $\theta = 7\pi/4\text{,}$ and $\theta = -11\pi/4\text{.}$ Include a sketch in each case.

Solution.

$\theta = 150^\circ$ is in Quadrant II and has reference angle $\bar\theta = 30^\circ\text{.}$

Table 9.37.

$\sin \theta = +\sin 30^\circ = \frac{1}{2}$	$\csc \theta = 2$
$\cos \theta = -\cos 30^\circ = -\frac{\sqrt{3}}{2}$	$\sec \theta = -\frac{2}{\sqrt{3}} = - \frac{2\sqrt{3}}{3}$
$\tan \theta = -\tan 30^\circ = -\frac{1}{\sqrt{3}} = - \frac{\sqrt{3}}{3}$	$\cot \theta = - \sqrt{3}$

$\theta = -2\pi/3$ is in Quadrant III and has reference angle $\bar\theta = \pi/3\text{.}$

Table 9.39.

$\sin \theta = -\sin \pi/3 = -\frac{\sqrt{3}}{2}$	$\csc \theta = -\frac{2}{\sqrt{3}} = - \frac{2\sqrt{3}}{3}$
$\cos \theta = -\cos \pi/3 = -\frac{1}{2}$	$\sec \theta = -2$
$\tan \theta = +\tan \pi/3 = \sqrt{3}$	$\cot \theta = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$

$\theta = 7\pi/4$ is in Quadrant IV and has reference angle $\bar\theta = \pi/4\text{.}$

Table 9.41.

$\sin \theta = -\sin \pi/4 = -\frac{\sqrt{2}}{2}$	$\csc \theta = -\frac{2}{\sqrt{2}} = - \frac{2\sqrt{2}}{2} = - \sqrt{2}$
$\cos \theta = +\cos \pi/4 = \frac{\sqrt{2}}{2}$	$\sec \theta = \sqrt{2}$
$\tan \theta = -\tan \pi/4 = -1$	$\cot \theta = -1$

$\theta = -11\pi/4$ is in Quadrant III and has reference angle $\bar\theta = \pi/4\text{.}$

Table 9.43.

$\sin \theta = -\sin \pi/4 =- \frac{\sqrt{2}}{2}$	$\csc \theta = -\sqrt{2}$
$\cos \theta = -\cos \pi/4 = -\frac{\sqrt{2}}{2}$	$\sec \theta = -\sqrt{2}$
$\tan \theta = +\tan \pi/4 = 1$	$\cot \theta = 1$

9.

Find all angles $0 \leq \theta \lt 2\pi$ satisfying $\sin(\theta) = -1\text{.}$

Solution.

The point $(0,-1)$ is the only point on the unit circle whose $y$-coordinate is $-1\text{.}$ This corresponds to $\theta = 3\pi/2\text{.}$ Draw a picture to confirm.

10.

Find all angles $0 \leq \theta \lt 2\pi$ satisfying $\cos(\theta) = 0\text{.}$

Solution.

The points $(0,1)$ and $(0,-1)$ are the only points on the unit circle whose $x$-coordinate is $0\text{.}$ These corresponds to $\theta = 0$ and $\theta = \pi\text{,}$ respectively. Draw a picture to confirm.

11.

Find all angles $0 \leq \theta \lt 2\pi$ satisfying $\tan(\theta) = -1\text{.}$

Solution.

The slope of a terminal ray is $-1$ for $\theta = 3\pi/4$ and $\theta = 7\pi/4\text{.}$ Draw a picture to confirm.

Exercises: Graphs.

These exercises address graphing sinusoidal curves and the graphs of other trigonometric functions.

12.

Practice drawing the graph of $y = \sin (\theta)\text{,}$ $y = \cos (\theta)\text{,}$ and $\tan(\theta)$ by considering the geometry of the unit circle.

Hint.

Remember that cosine is the $x$-coordinate and sine is the $y$-coordinate of the point on the unit circle determined by $\theta\text{.}$ Tangent is the slope of the terminal ray.

13.

Sketch the graphs of $y = - 2 \cos (\theta)\text{,}$ $y = \cos(\theta)-2\text{,}$ $y = \cos(2\theta)\text{,}$ and $y = \cos(\theta/2)\text{.}$

Solution.

$y=-2\cos\theta$ is the graph of cosine reflected over the horizontal axis and stretched vertically by a factor of 2 to give an amplitude of 2.

Figure 9.44.
$y=\cos\theta-2$ is the graph of cosine translated down 2 units

Figure 9.45.
$y=\cos(2\theta)$ is the graph of cosine stretched horizontally by a factor of 1/2 resulting in a period of $\pi\text{.}$

Figure 9.46.
$y=\cos(\theta/2)$ is the graph of cosine stretched horizontally by a factor of 2 resulting in a period of $4\pi\text{.}$

Figure 9.47.

14.

Sketch one period of $y=2\sin\left(3t-\frac{\pi}{4}\right)\text{.}$ Identify the amplitude, period, and phase shift.

Hint.

First solve $3t-\frac{\pi}{4} = 0$ and $3t-\frac{\pi}{4} = 2\pi$ for $t$ to find where one period begins and ends, respectively.

Solution.

To find where a period begins, solve

\begin{equation*} 3t - \frac{\pi}{4} = 0 \Rightarrow t = \frac{\pi}{12}. \end{equation*}

To find where this same period ends, solve

\begin{equation*} 3t - \frac{\pi}{4} = 2\pi \Rightarrow t = \frac{3\pi}{4}. \end{equation*}

We can plot this one period

to see that its the graph of sine shifted $\pi/12$ units to the right with a period of $3\pi/4 - \pi/12= 2\pi/3$ and an amplitude of 2.

15.

Sketch one period of $y=-\cos\left(2\left(t+\frac{\pi}{6}\right)\right)\text{.}$

Hint.

First solve $2\left(t+\frac{\pi}{6}\right) = 0$ and $2\left(t+\frac{\pi}{6}\right) = 2\pi$ for $t$ to find where one period begins and ends, respectively.

Solution.

To find where a period begins, solve

\begin{equation*} 2\left(t+\frac{\pi}{6}\right) = 0 \Rightarrow t = -\pi/6. \end{equation*}

To find where this same period ends, solve

\begin{equation*} 2\left(t+\frac{\pi}{6}\right) = 2\pi \Rightarrow t = 5\pi/6. \end{equation*}

We can plot this one period

to see that its the graph of cosine reflected over the $t$-axis, shifted $\pi/6$ units to the left with a period of $5\pi/6 - (-\pi/6)= \pi$ and an amplitude of 1. the peak occurs at the midpoint of $(5\pi/6 + (-\pi/6))/2 = \pi/3\text{.}$

16.

Sketch one period of $y = \tan(2x)\text{.}$ Label the vertical asymptotes and at least three points on the graph for scale.

Solution.

The graph of $y = \tan \theta$ has asymptotes where $\theta = \pm \pi/2\text{.}$ So if $2x = \pm \pi/2 \Rightarrow x = \pm \pi/4$ we will see asymptotes on $y = \tan(2x)\text{.}$ This means the period shrinks to $\pi/2\text{.}$

17.

Use the graph of $y = \sin(\theta)$ to help you sketch the graph of its reciprocal $y = \csc(\theta)\text{.}$

Solution.

Recall that $\csc\theta = \frac{1}{\sin\theta}\text{.}$ Think about what this means:

When sine is small (close to zero), cosecant will be large;
When sine is zero, cosecant will be undefined (vertical asymptote);
When sine is negative, cosecant will be negative.

Exercises: Identities.

These exercises emphasize use of some important trigonometric identities. Review Appendix A of Anton (Handout). Here’s a summary of summary important identities. Don’t feel obligated to memorize the Addition Formulas.

Table 9.52.

Ratio Identities
\begin{equation} \tan \theta = \frac{\sin \theta}{\cos \theta} \end{equation}		\begin{equation} \cot \theta = \frac{\cos \theta}{\sin \theta} \end{equation}
Reciprocal Identities
\begin{equation} \csc \theta = \frac{1}{\sin \theta} \end{equation}	\begin{equation} \sec \theta = \frac{1}{\cos \theta} \end{equation}		\begin{equation} \cot \theta = \frac{1}{\tan \theta} \end{equation}
Pythagorean Identity
\begin{equation} \sin^2 (\theta) + \cos^2 (\theta) = 1 \end{equation}
Opposite Angle Identities
\begin{equation} \cos(-\theta) = \cos(\theta) \end{equation}		\begin{equation} \sin(-\theta) = - \sin(\theta) \end{equation}
Addition Formulas
\begin{equation} \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \end{equation}
\begin{equation} \cos(\alpha+\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \end{equation}

18.

Use the the appropriate identities to simplify the following expression as much as possible.

\begin{equation*} \frac{\tan \theta \, \csc^3 \theta}{\cot^4 \theta \, \sin^5 \theta\, (1-\sin^2 \theta)} \end{equation*}

Your final answer should not include any ratios.

Answer.

Reciprocal identities will be helpful. Also, $1-\sin^2 \theta = \cos^2\theta\text{,}$ by the Pythagorean Identity.

\begin{equation*} \frac{\tan \theta \, \csc^3 \theta}{\cot^4 \theta \, \sin^5 \theta\, (1-\sin^2 \theta)} = \csc^3 \theta \sec^7 \theta \end{equation*}

19.

Suppose $\cos(\theta) = 0.3$ and $\theta$ is in Quadrant IV. Find the sine of the $\theta$ using the Pythagorean Identity.

Answer.

\begin{equation*} \sin(\theta) = - \sqrt{1-(0.3)^2} \approx - 0.9539 \end{equation*}

20.

Starting with the identity $\sin^2 \theta + \cos^2 \theta = 1\text{,}$ derive two similar identities involving tangent and cotangent, respectively.

Hint.

Divide both sides by $\cos^2\theta$ to see that

\begin{equation*} \tan^2 \theta + 1 = \sec^2 \theta \end{equation*}

Divide both sides by $\sin^2\theta$ to see that

\begin{equation*} 1+\cot^2 \theta = \csc^2 \theta \end{equation*}

21.

Use the Addition Formulas and the Opposite Angle Identities to derive the Difference Formulas

\begin{equation*} \sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \quad \text{and} \quad \cos(\alpha-\beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta. \end{equation*}

Hint.

Write the difference of angles as a sum $\sin(\alpha - \beta) = \sin(\alpha +(-\beta))\text{.}$

22.

Use the Difference Formulas above and the Special Triangles to find the exact values of $\sin(15^\circ)$ and $\cos(15^\circ)\text{.}$

Hint.

$15^\circ = 45^\circ - 30^\circ$ and the exact values of these can be found from the special triangles.

23.

Use the Addition Formulas to derive the following Double Angle Identities

\begin{equation*} \sin (2\theta) = 2\sin\theta \cos\theta \quad \text{and} \quad \cos (2\theta) = \cos^2 \theta - \sin^2 \theta. \end{equation*}

Hint.

Write the double angle as a sum $\sin (2\theta) = \sin (\theta + \theta)\text{.}$

24.

Use the Double Angle Identity for Cosine above to derive the Half-Angle Identities

\begin{equation*} \cos(x/2) = \pm \sqrt{\frac{1+\cos x}{2}} \quad \text{and} \quad \sin(x/2) = \pm \sqrt{\frac{1-\cos x}{2}}. \end{equation*}

Solution.

I’ll do one. From the double angle identity:

\begin{align*} \cos(2\theta) &= \cos^2 \theta - \sin^2 \theta\\ &= 1-\sin^2 \theta - \sin^2 \theta\\ \cos(2\theta)&= 1-2\sin^2 \theta \end{align*}

Solve this last equation for $\sin^2 \theta\text{,}$

\begin{equation*} \sin^2 \theta = \frac{1-\cos(2\theta)}{2} \end{equation*}

Thus,

\begin{equation*} \sin \theta =\pm\sqrt{\frac{1-\cos(2\theta)}{2}}, \end{equation*}

where the sign is determined by the quadrant $\theta$ is in. Let $\theta = x/2\text{,}$ then $2\theta = x$ and

\begin{equation*} \sin (x/2) =\pm\sqrt{\frac{1-\cos(x)}{2}}. \end{equation*}

Prev TopNext

\(\sin \theta = \frac{-1}{\sqrt{17}}= -\frac{\sqrt{17}}{17}\)	\(\csc \theta = \frac{\sqrt{17}}{-1} = - \sqrt{17}\)
\(\cos \theta = \frac{4}{\sqrt{17}}=\frac{4\sqrt{17}}{17}\)	\(\sec \theta = \frac{\sqrt{17}}{4}\)
\(\tan \theta = -\frac{1}{4}\)	\(\cot \theta = \frac{4}{-1}=-4\)

\(\sin \theta = \frac{-1}{\sqrt{17}}= -\frac{\sqrt{17}}{17}\)	\(\csc \theta = \frac{\sqrt{17}}{-1} = - \sqrt{17}\)
\(\cos \theta = \frac{4}{\sqrt{17}}=\frac{4\sqrt{17}}{17}\)	\(\sec \theta = \frac{\sqrt{17}}{4}\)
\(\tan \theta = -\frac{1}{4}\)	\(\cot \theta = \frac{4}{-1}=-4\)

\(\sin \theta = +\sin 30^\circ = \frac{1}{2}\)	\(\csc \theta = 2\)
\(\cos \theta = -\cos 30^\circ = -\frac{\sqrt{3}}{2}\)	\(\sec \theta = -\frac{2}{\sqrt{3}} = - \frac{2\sqrt{3}}{3}\)
\(\tan \theta = -\tan 30^\circ = -\frac{1}{\sqrt{3}} = - \frac{\sqrt{3}}{3}\)	\(\cot \theta = - \sqrt{3}\)

\(\sin \theta = -\sin \pi/3 = -\frac{\sqrt{3}}{2}\)	\(\csc \theta = -\frac{2}{\sqrt{3}} = - \frac{2\sqrt{3}}{3}\)
\(\cos \theta = -\cos \pi/3 = -\frac{1}{2}\)	\(\sec \theta = -2\)
\(\tan \theta = +\tan \pi/3 = \sqrt{3}\)	\(\cot \theta = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}\)

\(\sin \theta = -\sin \pi/4 = -\frac{\sqrt{2}}{2}\)	\(\csc \theta = -\frac{2}{\sqrt{2}} = - \frac{2\sqrt{2}}{2} = - \sqrt{2}\)
\(\cos \theta = +\cos \pi/4 = \frac{\sqrt{2}}{2}\)	\(\sec \theta = \sqrt{2}\)
\(\tan \theta = -\tan \pi/4 = -1\)	\(\cot \theta = -1\)

\(\sin \theta = -\sin \pi/4 =- \frac{\sqrt{2}}{2}\)	\(\csc \theta = -\sqrt{2}\)
\(\cos \theta = -\cos \pi/4 = -\frac{\sqrt{2}}{2}\)	\(\sec \theta = -\sqrt{2}\)
\(\tan \theta = +\tan \pi/4 = 1\)	\(\cot \theta = 1\)